Physicspedia: 2012

สัมพัทธภาพทั่วไป หรือ ทฤษฎีสัมพัทธภาพทั่วไป (อังกฤษ: General relativity หรือ General Theory of Relativity) คือทฤษฎีเชิงเรขาคณิตของความโน้มถ่วงและเอกภพวิทยา เสนอโดยอัลเบิร์ต ไอน์สไตน์ใน พ.ศ. 2458
ใจความสำคัญในทฤษฎีสัมพัทธภาพทั่วไปคือการตกเสรี (freefall) นั้นที่จริงแล้วคือกิริยาการเฉื่อยแบบหนึ่ง ซึ่งหมายความว่าความโน้มถ่วงนั้นไม่ได้ขึ้นอยู่กับแรงที่กระทำ เช่นโดยแทนที่การที่คนยืนอยู่บนพื้นโลกนั้นคือการ ที่พื้นโลกรองรับ "แรงโน้มถ่วง" เอาไว้ซึ่งก่อให้เกิดการเร่งทางฟิสิกส์อย่างต่อเนื่องซึ่งแทนที่จะรอบรับแรงโน้มถ่วงธรรมดา ๆ มันจะก่อให้เกิดค่าความต้านเชิงกลศาสตร์บนพื้นที่ที่คนกำลังยืนอยู่^[1]

Contents1 Tensor Analysis
     1.1 Metric Tensor
          1.1.1 Einstein Notation
          1.1.2 Kronecker Delta
          1.1.3 Metric Tensor of Polar Coordinate
          1.1.4 Inverse Metric
     1.2 Covariant Derivative
     1.3 Christoffel Symbols
2 Flat Space and Curved Space
     2.1 Flat Space
     2.2 Curved Space
     2.3 Singularity
     2.4 Parallel Transport
     2.5 Geodesics
     2.6 Curvature
          2.6.1 Sign of Curvature
3 Einstein Field Equation
     3.1 Riemann Curvature Tensor
          3.1.1 General Definition of Curvature
     3.2 Ricci Tensor and Ricci Scalar
          3.2.1 Ricci Tensor
          3.2.2 Ricci Scalar
     3.3 Energy-Momentum Tensor
          3.3.1 4-Current
          3.3.2 4-Momentum
          3.3.3 T^μν
     3.4 Slow & Weak-Field Approximation
     3.5 Einstein Field Equation
     3.6 Schwarzschild Solution
     3.7 Black Hole
          3.7.1 Non-rotating Uncharged Black Hole
          3.7.2 Rotating Uncharged Black Hole
          3.7.3 Non-rotating Charged Black Hole
          3.7.4 Rotating Charged Black Hole
     3.8 Cosmological Constant

Tensor Analysis

Metric Tensor
ดูที่ Metric Tensor
พิจารณาจุดสองจุดใดๆบนพิกัดคาร์ทีเชี่ยน เราสามารถหาระยะระหว่างจุดได้จากสมการ
$\Delta s^2=\Delta x^2+\Delta y^2+\Delta z^2$
หรือถ้าหากเรานิยาม coordinate ทั้งสามใหม่ว่า Δx=Δx¹, Δy=Δx² และ Δz=Δx³ (Δxⁱ ในที่นี้ไม่ได้หมายถึง Δx ยกกำลัง i แต่อย่างใด เป็นเพียงสัญลักษณ์แสดงเท่านั้น) เราจะเขียนสมการข้างต้นใหม่ได้ว่า
$\Delta s^2=(\Delta x^1)^2+(\Delta x^2)^2+(\Delta x^3)^2=\sum_{i=1}^{3}\Delta x^i\Delta x^i$
Einstein Notation
ดูที่ Einstein notation
ในสัมพัทธภาพทั่วไป เรานิยมลดรูปสมการที่ติดเครื่องหมาย summation Σ โดยมีหลักการง่ายๆ 3 ข้อ
- ให้ตัดสัญลักษณ์ sigma ออกจากสมการ เช่น b_n= Σa_mne^m กลายเป็น b_n= a_mne^m
- index ที่ซ้ำกันในแต่ละเอกนาม เรียกว่า summation index หมายถึง index ที่เคยอยู่ใต้เครื่องหมาย sigma กล่าวคือ
$a_mb^m\rightarrow \sum_{m} a_mb^m$
- summation index ต้องอยู่ในตำแหน่งตรงข้ามกันเท่านั้น(ตัวหนึ่งอยู่บน เรียกว่า upper index ตัวหนึ่งอยู่ล่าง เรียกว่า lower index)
กล่าวคือ a_mne^m ถูกต้อง, a_mne^meⁿ ถูกต้อง, a^mb^m ผิด, a_mne^mb^m ไม่นิยมใช้

Kronecker Delta
สำหรับสมการหาระยะทางระหว่างสองจุด เราสามารถเขียนใหม่ตามหลักของ Einstein Notation ได้ว่า
$\Delta s^2=\delta_{mn}\Delta x^m \Delta x^n$
จากสมการ สัญลักษณ์ δ_mn มีนิยามโดย
$\delta_{mn}=\left\{\begin{matrix} 1; m=n\\0; m\not=n \end{matrix}\right.$
ดังนั้น หากพิจารณาอย่างถี่ถ้วนแล้ว จะพบว่าสมการดังกล่าวคืออย่างเดียวกันกับสมการในรูปของเครื่องหมาย sigma นี่เอง
เราเรียก δ_mn (อ่านว่า kronecker delta หรือเรียกสั้นๆว่า delta)ว่าเป็น metric tensor ของ Cartesian coordinate
นอกจากนี้ เรายังสามารถเขียน δ_mn ได้ในรูบของ matrix (ระวัง: metric tensor ไม่ใช่ matrix แต่สามารถเขียนได้ในรูปของ matrix ในบางครั้ง)
$\delta_{mn}=\begin{pmatrix} 1 & 0 & 0\\ 0 & 1 & 0\\ 0 & 0 & 1 \end{pmatrix}$
เมื่อ mn หมายถึงสมาชิกแถวที่ m คอลัมน์ที่ n ของ matrix ดังกล่าว (สาเหตุที่ matrix มีขนาดเป็น 3x3 เพราะระบบที่เรากำลังศึกษาเป็นระบบ 3 มิติ)

Metric Tensor of Polar Coordinate
ตัวอย่างที่ดีของการหา metric tensor คือระบบพิกัดเชิงขั้ว เนื่องจากระยะห่างระหว่างจุดใดๆ บนระบบพิกัดเชิงขั้ว สามารถเขียนได้ในรูป
$ds^2=dr^2+r^2d\theta^2$
เมื่อมุม θ และรัสมี r เป็น coordinate พื้นฐานของระบบพิกัดเชิงขั้ว ดังนั้น หากเราตั้งค่าให้ dr=dx¹ และ dθ=dx² จะได้ metric tensor คือ
$g_{mn}=\begin{pmatrix} 1 & 0\\ 0 & r^2 \end{pmatrix}$
exercise: จงแสดงว่า metric ของระบบพิกัดเชิงขั้วมีลักษณะดังกล่าว

Inverse Metric
คือ tensor อีกชนิดหนึ่ง(upper index สองตัว) ซึ่งทำหน้าที่สลับตำแหน่งของ index มีสมบัติพื้นฐานดังนี้
$1.\; \; g^{mn}A_{m}\,^{l}=A^{nl}$
$2.\; \; g^{mn}g_{mn}=\delta_n^n=\delta_1^1+\delta_2^2+\delta_3^3+...=\textup{dimension}$
และสมบัติอื่นๆซึ่งต้องศึกษากันต่อไป

Covariant Derivative
ให้ x แทนตำแหน่งใดๆบน space d มิติ (x ไม่ใช่ชื่อแกน)
$x=\begin{pmatrix} x^1\\ x^2\\ \vdots \\ x^d \end{pmatrix}$
จะกำหนดสนามเวกเตอร์ V(x) บน space นี้ได้ว่า
$V(x)=\begin{pmatrix} V^1(x)\\ V^2(x)\\ \vdots \\ V^d(x)\end{pmatrix}$

พิจารณาการเปลี่ยนแปลงของ V^m(x) ไปตามแนวแกน x^k ใดๆ สามารถหาได้จากสมการ
$\textup{changing rate}=\frac{\partial }{\partial x^k}V^m=T_k\,^m$
เมื่อ T_k^m คือปริมาณบางอย่างซึ่งถูก label ด้วย index ทั้งสองตัว(ปริมาณ index ที่ไม่ใช่ summation index ของทั้งสองฟากสมการต้องมีเท่าเดิมเสมอ ในที่นี้คือ m และ k) ปัญหาของเราก็คือ หากเราเปลี่ยน coordinate x ไปเป็น y เช่น จากคาร์ทีเชี่ยนไปเป็นเชิงขั้ว (ไม่ใช่เปลี่ยนจากแกน x ไปเป็น แกน y) สมการจะยังเหมือนเดิมหรือเปล่า
$\frac{\partial }{\partial x^k}V^m_{(x)}=T_k\,^m_{(x)}\overset{?}{\Rightarrow } \frac{\partial }{\partial y^k}V^m_{(y)}=T_k\,^m_{(y)}$
เราสามารถลองคำนวณดูได้ดังนี้ เริ่มจากการแปลง coordinate จาก x ไปสู่ y ทำได้จาก
$V^m_{(x)}=\frac{\partial x^m}{\partial y^n}V^n_{(y)}$
หรือ
$V_{m(x)}=\frac{\partial y^n}{\partial x^m}V_{n(y)}$
เรียก V^m ว่า contravariance vector และเรียก V_m ว่า covariance vector (ดู wikipedia:Covariance_and_contravariance_of_vectors) แต่ในกรณีนี้เราจะศึกษาเฉพาะ contravariance vector เป็นหลัก
นอกจากนี้เรายังสามารถเปลี่ยน coordinate ของ tensor T_k^m ได้ด้วย จากสมการ
$T_k\,^m_{(x)}=\frac{\partial V^m_{(x)}}{\partial x^k}\Rightarrow T_k\,^m_{(y)}=\frac{\partial y^m}{\partial x^n}\frac{\partial x^r}{\partial y^k}T_r\,^n_{(x)}=\frac{\partial y^m}{\partial x^n}\frac{\partial x^r}{\partial y^k}\frac{\partial V^n_{(x)}}{\partial x^r}=\frac{\partial y^m}{\partial y^k}\frac{\partial V^n_{(x)}}{\partial x^n}$
แต่ทว่า หากเราหันมาแปลง coordinate ของ V แทน เราจะพบว่า
$T_k\,^m_{(y)}=\frac{\partial}{\partial y^k} V^m_{(y)}=\frac{\partial}{\partial y^k}(\frac{\partial y^m}{\partial x^n}V^n_{(x)})=\frac{\partial y^m}{\partial y^k}\frac{\partial V^n_{(x)}}{\partial x^n}+V^n_{(x)}\frac{\partial^2 y^m}{\partial y^k\partial x^n}$
ซึ่ง
$\frac{\partial y^m}{\partial y^k}\frac{\partial V^n_{(x)}}{\partial x^n}+V^n_{(x)}\frac{\partial^2 y^m}{\partial y^k\partial x^n}\neq \frac{\partial y^m}{\partial y^k}\frac{\partial V^n_{(x)}}{\partial x^n}$

ดังนั้น อนุพันธ์ทั่วไปของ Vector (และ Tensor) จึงไม่ใช่ตัวดำเนินการพื้นฐาน เพราะทำให้ได้ค่าไม่เท่าเดิมเมื่อเปลี่ยน coordinate เราจึงจำเป็นต้องนิยาม อนุพันธ์ ชนิดใหม่ ซึ่งให้ผลเดิมเสมอเมื่อเปลี่ยน coordinate เราเรียกอนุพันธ์ชนิดใหม่นี้ว่า covariant derivative
$\nabla_kV^m_{(x)}=T_k^m\Rightarrow \nabla_kV^m_{(y)}=T_k^m$

Christoffel Symbols
สำหรับ covariant derivative ของ V^m เราสามารถเขียนได้ว่า
$\nabla_kV^m=\partial_kV^m+\Gamma^m_{kp}V^p$
สัญลักษณ์ ∂_k ในที่นี้หมายถึงการย่อรูปของการ derivative แบบทั่วไปลง Gamma(Γ) ที่เห็นเป็นเพียงสัญลักษณ์ตัวหนึ่งซึ่งสร้างขึ้นมาเพื่อดุลย์ให้สมการเป็นจริงในทุกๆ coordinate เรียกสัญลักษณ์นี้ว่า Christoffel Symbol
เราสามารถแสดงให้เห็นผ่านการคำนวณที่ซับซ้อนได้ว่า
(ดู การหาค่า Christoffel Symbol)
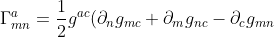$\Gamma_{mn}^a=\frac{1}{2}g^{ac}(\partial_ng_{mc}+\partial_mg_{nc}-\partial_cg_{mn})$
สำหรับ metric และ inverse metric g ใดๆ (หมายเหตุ ในกรณีส่วนใหญ่ เรามักจะไม่มองว่าสองตัวนี้แตกต่างกัน การใช้จึงแล้วแต่บริบท ซึ่งจะได้เห็นกันต่อไป)

สำหรับรูปทั่วไปของ covariant derivative นิยามโดย
$\nabla_kV^{a_1a_2...}_{b_1b_2...}=\partial_kV^{a_1a_2...}_{b_1b_2...}+\Gamma^m_{ka_1}V^{da_1a_2...}_{b_1b_2...}+\Gamma^m_{ka_2}V^{a_1d...}_{b_1b_2...}+...-\Gamma^d_{kb_1}V^{a_1a_2...}_{db_2...}-\Gamma^d_{kb_2}V^{a_1a_2...}_{b_1d...}$

Flat Space and Curved Space

ในการศึกษา Tensor Geometry เราจำแนกพื้นผิวออกเป็นสองจำพวก คือ พื้นเรียบ(flat surface) กับ พื้นโค้ง(curved surface)
Flat Space
สำหรับพื้นผิวเรียบ coordinate ที่พื้นฐานที่สุดซึ่งไม่มีในพื้นผิวโค้งคือระบบพิกัดคาร์ทีเชี่ยน มีสมบัติ(ซึ่งเห็นได้ชัด)คือ coordinate จะดูเหมือนเดิมในทุกๆตำแหน่ง(เป็นตารางไกลไปสุดลุกหูลุกตา) หรือพูดอีกนัยหนึ่งได้ว่า :: ใน flat space จะต้องมีอย่างน้อยหนึ่ง coordinate ซึ่ง metric มีสมบัติคือ
$\frac{\partial g_{mn}}{\partial x^k}=0$

Curved Space
ในพื้นผิวโค้งเราก็มีนิยามเช่นกัน กล่าวได้ว่า :: บนพื้นผิวโค้ง จะต้องมีจุดอย่างน้อยหนึ่งจุด(เช่นจุดเปลี่ยนเว้า) และ coordinate อย่างน้อยหนึ่ง coordinate ซึ่งมีสมบัติคือ
$(\frac{\partial g_{mn}}{\partial x^k})_{\textup{at point} \textbf{P}}=0$
ยกตัวอย่างเช่น ยอดโดม, ทุกบริเวณของผิวทรงกลม, ทุกบริเวณของผิวทรงกรวยที่ไม่ใช่ยอดกรวย เป็นต้น
exercise: จงอธิบายตัวอย่างข้างต้นว่าทำไมถึงมีสมบัติดังกล่าว

Singularity
ในเชิงเรขาคณิต singularity คือจุดซึ่งมีสมบัติคือ ไม่มี coordinate ใดสามารถทำให้
$(\frac{\partial g_{mn}}{\partial x^k})_{\textbf{P }\textup{is singularity}}=0$

Parallel Transport
ดูที่ Parallel Transport
หมายถึงการเคลื่อนย้าย vector ใดๆไปตามเส้นทางที่กำหนด โดยมีเงื่อนไขคือการทำให้ vector นั้นขนานกับ vector เดิมตลอดเส้นทาง

Parallel transport ของ vector ไปตามเส้นจะทำให้ vector ตัวนั้นขนานกับตัวเองไปตลอดเส้น

การแปลงแบบนี้ เราสามารถพูดอีกนัยหนึ่งได้ว่า Vector จะดูไม่เปลี่ยนแปลงหากเราเดินไปตามเส้น นั่นคือ covariant derivative ของ vector จะเท่ากับศูนย์
$\nabla_sV^m=\frac{\partial V^m}{\partial s}+\Gamma^m_{np}V^n\frac{\mathrm{d} x^p}{\mathrm{d} s}=0$
สำหรับเส้นทาง s ใดๆ ซึ่งทำให้ได้นิยามของ parallel transport คือ
$\textup{parallel transport : }\frac{\partial V^m}{\partial s}=-\Gamma^m_{np}V^n\frac{\mathrm{d} x^p}{\mathrm{d} s}$

Geodesics
ดูที่ Geodesic (general relativity)
พิจารณา tangent vector ของเส้นทาง s
$V^m=\frac{\mathrm{d} x^m}{\mathrm{d} s}$
จะได้การเปลี่ยนแปลงไปตาม s ของ tangent vector เองก็คือ
$\nabla_sV^m=\nabla_s\frac{\mathrm{d} x^m}{\mathrm{d} s}$
พิจารณากรณีพิเศษซึ่ง tangent vector จะดูเหมือนเดิมตลอดเมื่อเคลื่อนไปตามแนว s นั่นคือ s จะต้องเป็นเส้นตรง(บนพื้นผิวเรียบ)นั่นเอง หรือในกรณีทั่วไป เราจะเรียกเส้นทาง s นี้ว่า Geodesics
$\nabla_sV^m=\nabla_s\frac{\mathrm{d} x^m}{\mathrm{d} s}=0$
หรือสามารถเขียนใหม่ได้ว่า
$\textup{Geodesics : }\frac{\partial^2 x^m}{\partial s^2}=-\Gamma^m_{ab}\frac{\mathrm{d} x^a}{\mathrm{d} s}\frac{\mathrm{d} x^b}{\mathrm{d} s}$
ยกตัวอย่างเช่น การโคจรของวัตถุรอบๆแหล่งกำเนิดสนามโน้มถ่วง เราจะเขียนสมการข้างต้นใหม่ได้ว่า
$\textup{Orbits : }\frac{\partial^2 x^m}{\partial \tau^2}=-\Gamma^m_{ab}\frac{\mathrm{d} x^a}{\mathrm{d} \tau}\frac{\mathrm{d} x^b}{\mathrm{d} \tau}$
เมื่อ τ คือ proper time เปรียบเสมือนเส้นทางการเคลื่อนที่ของวัตถุบน space-time diagram (มิติตำแหน่ง + มิติเวลา)

Curvature
จำเป็นหรือไม่ที่ vector ที่ผ่านการ parallel transport เป็นวงกลมกลับมาที่จุดเดิม จะมีทิศทางเดิมเสมอ? คำตอบคือไม่จำเป็น หากระบบที่เรากำลังศึกษาเป็นระบบที่มีความโค้ง

หลังจากทำให้กรวยกลายเป็นแผ่นแบน(flat space) และทำการเลื่อนขนาน vector ผ่านยอดกรวย (tip) จนกลับมาที่เดิม พบว่ามุมที่ vector มีเปลี่ยนไปจากเดิมเมื่อม้วนกรวยกลับไปเป็นรูปทรงสามมิติอีกครั้ง

ในกรณีทั่วไป เราจะศึกษาพื้นผิวโค้งที่ไม่ใช่รูปกรวย กล่าวคือ เมื่อเราเลื่อนขนาน vector รอบจุดหนึ่งๆแล้วมุมที่ได้ต่างจากเดิม เราจะเรียกพื้นผิวนั้นๆว่าเป็นพื้นผิวโค้ง (curved space)

Sign of Curvature
ในทางเรขาคณิต ความโค้งจำแนกได้เป็นสองชนิด

หากเลื่อนขนาน vector จนครบวงแล้วพบว่าทิศทางของ vector ลัพท์หมุนไปทิศเดียวกับการเลื่อนขนาน(บนซ้าย) เราจะเรียกพื้นผิวโค้งนี้ว่ามีค่าความโค้ง (R: Curvature Scalar) เป็นบวก ในทางกลับกัน หากการหมุนมีทิศตรงข้ามกับการเลื่อนขนานเช่นในพื้นผิวแบบอานม้า(บนขวา)จะเรียกว่ามีค่าความโค้งเป็นลบ ที่น่าสนใจคือรูปทรงแบบโดนัท(แบบ toroid) มีพื้นผิวโค้งของทั้งสองแบบในรูปทรงเดียวกัน

Einstein Field Equation

ทฤษฎีสัมพัทธภาพทั่วไปเป็นการศึกษาปัญหาสองอย่าง 1) มวลส่งผลอย่างไรต่อความโค้ง และ 2) ความโค้งส่งผลอย่างไรต่อการเคลื่อนที่ของมวล ซึ่งปัญหาที่สองเราได้แก้ไปแล้วจากการหาสมการ Geodesics ใน spacetime โค้ง (การโคจร) แต่ปัญหาแรกต้องแก้โดยใช้สมการสนามของไอน์สไตน์ในการช่วยเหลือ สมการสนามไอน์สไตน์ประกอบด้วย2ส่วนหลัก คือส่วนความโค้งของ spacetime และส่วนพลังงานและมวล
Riemann Curvature Tensor
General Definition of Curvature
ในกรณีทั่วไป เราจะพูดถึงพื้นที่ซึ่งเล็กมากๆ กำหนดโดยแกน x^μและ x^νใดๆ ดังนั้นสมการควรจะอยู่ในรูป
ผลต่างเวกเตอร์ = dx^μdx^ν•(เวกเตอร์ต้นแบบ)•(ปริมาณบางอย่าง)
นั่นคือ
$\delta V^\sigma=\mathrm{d}x^\mu\mathrm{d}x^\nu V^\rho \mathcal{R}^\sigma_{\mu\nu\rho}$
ในที่นี้ R ก็คือสิ่งที่ช่วยบ่งบอกความโค้งของพื้นผิวที่กำลังศึกษา เรียกว่า Riemann Curvature Tensor ซึ่งเราสามารถแสดงให้เห็นผ่านการคำนวณที่ซับซ้อนได้ว่า
(ดู การหาค่า Riemann Tensor)
$\mathcal{R}^\sigma_{\mu\nu\rho}=\partial_\nu\Gamma^\sigma_{\rho\mu}-\partial_\rho\Gamma^\sigma_{\nu\mu}+\Gamma^\sigma_{\nu\lambda}\Gamma^\lambda_{\rho\mu}-\Gamma^\sigma_{\rho\lambda}\Gamma^\lambda_{\nu\mu}$

Ricci Tensor and Ricci Scalar
จากนิยามของ Riemann Tensor ที่ได้กล่าวมาแล้ว เราสามารถนิยามปริมาณอีกสองชนิดซึ่งมีประโยชน์มากกว่าได้คือ
Ricci Tensor
$R_{\mu\nu}=\mathcal{R}^\sigma_{\mu\sigma\nu}$
Ricci Scalar
บางครั้งเรียก Curvature Scalar
$R=g^{\mu\nu}R_{\mu\nu}=g_{\mu\nu}R^{\mu\nu}$

น่าสังเกต: Γ^κ_λη เป็นฟังก์ชันของ ∂g_σρ ซึ่งR_μν ก็เป็นฟังก์ชันของ ∂Γ^α_βγ อีกที ดังนั้น R_μν เป็นฟังก์ชันของ ∂∂g_φψ

Energy-Momentum Tensor
ดูที่ Four-vector
4-Current
ในทางกลศาสตร์ เราสามารถเขียนความหนาแน่น ρ ของมวล m ได้ว่า
$\rho=\frac{\mathrm{d} m}{\mathrm{d} V}=\frac{\partial^3 m}{\partial x\partial y\partial z}$

และกระแส j ของมวล m เมื่อไหลไปผ่านพื้นที่ A เขียนได้ว่า
$j_z=\frac{\mathrm{d} }{\mathrm{d} t}(\frac{\mathrm{d} m}{\mathrm{d} A})=\frac{\partial^3 m}{\partial t\partial x\partial y}$

นั่นเอง หากเราเปรียบเทียบปริมาณเหล่านี้กับ 4-Vector ใน space-time เราสามารถนิยาม 4-Current ได้ว่า
$J=\begin{pmatrix} \rho\\ j_x\\ j_y\\ j_z \end{pmatrix}$
หรือเขียนในรูป Tensor ได้ว่า
$J^\mu = \mathrm{d}x^\mu\partial_V m$
เมื่อ V คือปริมาตรใน 4 มิติ และ x⁰=t

4-Momentum
ทำนองเดียวกัน เราสามารถนิยาม 4-Vector ของ Momentum-Energy ได้เช่นกัน
$\textup{P}=\begin{pmatrix} E/c^2\\ p_x\\ p_y\\ p_z \end{pmatrix}=\begin{pmatrix} E\\ p_x\\ p_y\\ p_z \end{pmatrix}_{setting\; c=1}$

T^μν
ดูที่ Stress–energy tensor
ในทฤษฎีสัมพัทธภาพทั่วไป มวล โมเมนตัม และพลังงานต่างก็ส่งผลต่อ spacetime ทั้งหมด ดังนั้นไอน์สไตน์จึงสนใจใน tensor อีกชนิดก็คือ Stress-energy tensor หรือในอีกชื่อหนึ่งคือ Energy-momentum tensor ซึ่งสนใจปริมาณจำพวก กระแสโมเมนตัม ความหนาแน่นโมเมนตัม กระแสพลังงาน ความหนาแน่นพลังงาน เป็นต้น ดังนั้นเราจะเขียน tensor นี้ได้ว่า
$T^{\mu\nu}=\mathrm{d}x^\nu\partial_VP^\mu$

องค์ประกอบต่างๆของ Energy-Momentum Tensor (จาก wikipedia)

Slow & Weak-Field Approximation
ดูที่ Field Equation
พิจารณาวัตถุเคลื่อนที่ไปตามแกน x และมีความเร็วต่ำมากเมื่อเทียบกับความเร็วแสง(ตั้งให้ c=1)
$\frac{\mathrm{d} x}{\mathrm{d} t}\ll 1$
นั่นเท่ากับเป็นการบอกว่า
$\mathrm{d} t\approx \mathrm{d} \tau\; \; \; \frac{\mathrm{d} x^i}{\mathrm{d} \tau}\approx 0$
ประยุกต์เข้ากับสมการ geodesics จะได้ว่า
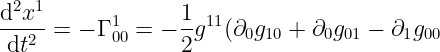$\frac{\mathrm{d}^2 x^1}{\mathrm{d} t^2}=-\Gamma^1_{00}=-\frac{1}{2}g^{11}(\partial_0g_{10}+\partial_0g_{01}-\partial_1g_{00})$
ที่ความเข้มสนามต่ำ เราสามารถประมาณ g_μν ได้ว่า
$g_{\mu\nu}\approx \eta_{\mu\nu}=\begin{pmatrix} 1 & 0 & 0& 0\\ 0 & -1& 0 &0 \\ 0& 0& -1&0 \\ 0& 0& 0 & -1 \end{pmatrix}$
ดังนั้นจะสรุปใหม่ได้ว่า
$\textup{slow\, \&\, weak-field\: approximation}:-\frac{1}{2}\frac{\partial g_{00}}{\partial x}=\frac{\mathrm{d}^2 x}{\mathrm{d} t^2}$

แต่กระนั้น Newtonian Physics กล่าวว่า
$\frac{\mathrm{d}^2 x}{\mathrm{d} t^2}=-\frac{\partial \Phi}{\partial x}$
สำหรับสนามโน้มถ่วง Φ
ดังนั้น เท่ากับว่า ที่สนามอ่อนๆและความเร็วต่ำ
$g_{00}_{(x)}\approx 2\Phi_{(x)}+\texttt{constant}$

Einstein Field Equation
ในสมการสนามของ Newton
$\partial^2_x\Phi=4\pi\rho G$
เราสามารถเขียนให้อยู่ในรูปของสมการแบบ Tensor ได้ว่า
$G^{\mu\nu}=8\pi GT^{\mu\nu}$
โดยใช้หลักที่ว่าถ้า m=E(ให้ c=1) แล้ว ρ=T⁰⁰
G^μνคือ Tensor บางอย่างที่สอดคล้องกับสมการสนามของ Newton ในกรณีที่ μ=0 และ ν=0
$G_{00}=2\partial^2_x\Phi=\partial^2_xg_{00}$

Einstein ให้ความเห็นว่า G^μν ควรมีบางอย่างเกี่ยวข้องกับ Ricci Tensor เราเรียก G^μνว่า Einstein Tensor ซึ่งในภายหลังเราพบว่า Tensor นี้มีนิยามคือ
(ดู การหาค่า Einstein Tensor)
$G^{\mu\nu}=R^{\mu\nu}-\frac{1}{2}g^{\mu\nu}R$
ทำให้สมการสนามของไอน์สไตน์มีรูปเต็มคือ
$\textup{Einstein\;Field\;Equation:\;}R^{\mu\nu}-\frac{1}{2}g^{\mu\nu}R=8\pi GT^{\mu\nu}$

Schwarzschild Solution
ในที่สุด Karl Schwarzschild ก็ได้แก้สมการสนามไอน์สไตน์ออกในกรณีของก้อนมวลนิ่งไม่หมุนที่บิดเบน spacetime ว่ารูปทรงของ spacetime ใน 4 มิติ จะมี metric เป็นไปตามสมการ
(ดู การพิสูจน์ Schwarzschild Metric)
$\begin{matrix} g_{\mu\nu}=\begin{pmatrix} 1-\frac{2GM}{r} & & & \\ & -(1-\frac{2GM}{r})^{-1}& & \\ & & -r^2& \\ & & & -r^2\textup{sin}^2\theta \end{pmatrix}\\ x^0=t,\;x^1=r,\;x^2=\theta,\;x^3=\phi \end{matrix}$
เมื่อ coordinate ทั้งสี่ตัวเป็น coordinate พื้นฐานของระบบพิกัดแบบทรงกลม 2GM ถูกเรียกว่าเป็น รัสมีของชวาร์ซ์ชิลด์ คือรัสมีที่ทำให้เกิดเป็นหลุมดำได้(ลองแทนค่าดู)

ผลของการบิดเบน spacetime ทำให้แสงสามารถเดินทางเป็นเส้นโค้งผ่านดาวฤกษ์ได้ และนี่คือที่มาของแรงโน้มถ่วงที่เรารู้จักกันดี

Black Hole
ในกรณีทั่วไป คำตอบของสมการสนามไอน์สไตน์จะถูกตีความว่าเป็นสมบัติของหลุมดำแต่ละชนิด ซึ่งมีดังต่อไปนี้
Non-rotating Uncharged Black Hole
ถูกกำหนดโดย Schwarzschild Solution
Rotating Uncharged Black Hole
ถูกกำหนดโดย Kerr Solution
Non-rotating Charged Black Hole
ถูกกำหนดโดย Reissner–Nordström Solution
Rotating Charged Black Hole
ถูกกำหนดโดย Kerr-Newman Solution

Cosmological Constant
ดูที่ Cosmological Constant

Physicspedia

Gravitational Red-shift Proof

Gravitational time dilation proof

ทฤษฎีสัมพัทธภาพทั่วไป